This blog is a chronicle of my exploration into Mixture of Experts (MOE), a machine learning architecture that employs a gating network to distribute input data to specialized expert sub-networks. Here, I will be documenting my experiences and insights as I delve into exploring and understanding how MOE work. The content will involve both theoretical and visual explanations.

I will give a brief intro to MOEs for the unacquainted. For details, definitely check out these wonderful blogs - cameronwolfe and huggingface. For the adventurous, you can look at the research paper: Outrageously Large Neural Networks.

Inspiration for the code used for this blog was taken from davidmrau and lucidrains.

Intro

Increase in capacity of LLM tends to result in consistent increase in performance. But increase in capacity of LLM have several limitations - mainly due to the compute resources required to run such a large model. MOE is a solution to the compute problem by creating parallel copies of dense layers called "experts". By limiting the computation to a fixed number of experts during any forward pass, the size can be increased while the computation stays constant (mostly). This can make inference significantly cheaper, which is very useful for models deployed in production.

The image below shows the MOE layers. The image is taken from the paper "Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer".

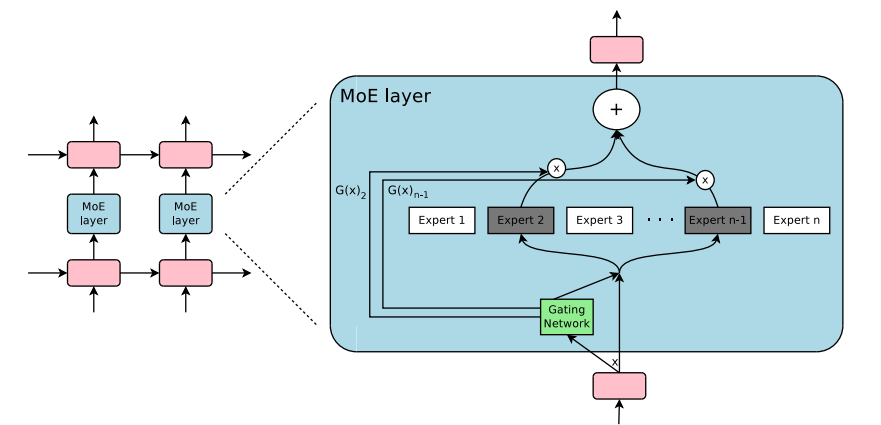
The MOE layer has a gate/router and experts. Given an input sample, the router determines the expert(s) the input will be sent to. The input is then passed through the chosen experts and the outputs of the experts are combined to form a single output.

The selection of experts is done by using the router to output a probability distribution over the experts and selecting the experts with highest probability. The same probability is used to weight the outputs of the experts before combining.

In the formula above,

1. is the output of router.
2. selects the top k values from and retains them, while setting the rest to zero. For example, .
3. Then finally, converts the given vector to probabilities.

The values from are used to combine the outputs of experts.

is the component of and is the output of the expert.

There is a major issue that needs to be addressed in MOEs before I proceed further. That is the distribution of data or tasks over the experts. We need a way to ensure that the inputs are equally distributed (mostly) amongst the experts to fully utilize the increased model capacity and this has to be incorporated into the router. We do this by adding an auxiliary loss to the final objective.

Where is the batch, is the Coefficient of Variation and is a hyperparameter to adjust the relative weighing of this loss in the final loss.

This minimization of this loss effectively tries to make the output distribution of the router as close to uniform as possible.

I've only touched the tip of the iceberg with this. There is a lot more to learn and understand about MOEs and I refer the reader to one of the blogs mentioned initially.

Experiments

Here, my goal is to understand the relationship between different hyperparameters and their effects on the resulting performance of an MOE.

MOEs have the following hyperparameters:

1. Number of experts (/): This is the number of individual experts our MOE will have.
2. : This is the number of "top" experts chosen for a forward pass
3. Loss coefficient (): The coefficient to tune the network loss with the router loss.

List of hyperparemeter values tested:

: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
∈ [1, min(num_experts, 4)]
: [0.0, 1e-05, 0.0001, 0.001, 0.01, 0.1, 1.0, 10.0]

Data: For all experiments henceforth, I use the MNIST dataset that contains images of singular digits (0-9) of size 28x28. I use the standard train and test split for the dataset: 60,000 samples for training and 10,000 for testing.

Model: The network itself consists of 2 parts: the router or gate, and the experts. The router is a linear layer with no bias and outputs a probability distribution over the experts. Each expert is a neural network with 2 layers: 784 --> 10 --> num_classes.

Loss: To train our model for classification, we use cross entropy loss as our "Network loss". Additionally, we add the "Gate loss" from above to the Network loss for end-to-end training.

Effect of lc

is the loss coefficient to balance the performance of MOE while maintaining a mostly uniform distribution among the individual experts.

First, let's fix and see the effect of on the results for different number of experts (). The value of is fixed to understand the effect of without a changing value of . The number of experts is varied from to 10.

For each value of and fixed , we construct 3 plots: Accuracy, Network loss and Gate loss. The plot for Accuracy shows the overall accuracy of the MOE on the test set for different number of experts. The plot for Network loss shows the changing values of the Network loss during training. Similarly, plot for Gate loss shows the changing values of Gate loss during training.

The average accuracy over the number of experts increases as increases. It is the maximum for and then falls for . For the "good" values of , we also see the increasing pattern of accuracy for increase in number of experts. For the lower values of , this trend is not observed, which implies that the results for these values have a fair bit of randomness involved in the final performance.

We see the explanation for this in the plots for gate loss and network loss - the two components of the MOE loss. With a low value of , more preference is given to network loss - this results in the gate not learning well how to route the inputs to the experts and hence results in inconsistent and detrimental behaviour. Hence, for low values of , the gate loss is very high and goes down as the is increased. On the contrary, for , the gate values are very small but the network loss has increased slightly, which leads to worsening performance of the individual experts.

Effect of k

Now, let's fix and see the effect of on the results. Similar to before, varies from to 10 but since the value of is changing for this experiment, the minimin value of also changes.

For , the results are nice and consistent. For , it doesn't work. This is because is needed to have non-zero derivatives with respect to the weights of the gate.

The paper Switch-Transformers propose a way to train MOEs with !

Analysis: Understanding the behaviour of experts

Here I want to try and understand what is happening inside the MOEs that is causing the increasing in performance. Either the classification accuracy for each digit is being increased equally (approx) or the accuracy for some classes is increasing a lot more than others.

Let's take a look at the classwise accuracy for different number of experts and compare to base model (with ne=1).

The plot above shows the improvement of class-wise accuracies for increasing number of experts compared to the base model (ne=1) shown in blue. Same for the plots below.

Classes 4, 6 and 9 are seeing almost the entirety of improvement! But this doesn't tell us how the misclassification is happening or being resolved.

Let's take a look at confusion matrices to understand the cause of misclassifications.

So it looks like 4 is being misclassified as 9, 6 is being misclassified as a lot of other numbers and 9 is being misclassified as 4 and 7.

The misclassification is overcome in MOEs, as expected! None of the classes are now performing worse than others.

Finally, let's see what exactly is happening within the experts - do the confusing classes get sent to the same experts?

The following plots show the distribution of input samples among the samples.

For very few experts (ne [2, 3]), we don't seem much specialization (specialization = experts learn to distinguish between fewer classes but perform better). All experts see samples from all classes. Therefore, the increase in performance in these cases is likely due to the increase in model capacity.

Now we see specializations starting to occur. Most samples from each class are now being divided between 2-3 experts. This is also likely why we see a prominent jump in performance from ne=3 ( 93.5%) to ne=4 ( 95%)!

We see another minor jump as the specializations start to look fairly well defined here.
Most interestingly, we see that the most confusing classes (4, 7 and 9) are being sent to the same expert for the best classification!

This is not a necessary phenomenon for increase in performance, as we see ne=4 and ne=5 don't have this behavior and neither does ne=8.

Regardless, this is a sufficient phenomenon and is really interesting to see that the a few of the experts can learn to specialize in the most confusing parts of the input space.

With increasing number of experts, we eventually hit the point of diminishing returns. Here, each expert specialises in close to 3 classes, while each class gets sent to about 2-4 experts.

Overall, for a small number of experts, the experts learn the entire task and as we increase the number of experts, the experts specialize in a few classes. Among the specializations, each expert learns to classify among a few classes only but there can be multiple experts specializing in the same class. Samples from each class gets sent only to a few experts - this number tends to increase as the total number of experts (ne) increases.

Final thoughts

Despite their impressive potential, Mixture-of-Experts (MOE) models remained relatively under the radar until recently. However, with the explosive growth of large language models (LLMs) and the desire to make them even larger and more knowledgeable, MOEs have finally stepped into the limelight.

Inspired by the recent surge of interest, I delved into the workings of MOEs using a simplified example. However, this is just the tip of the iceberg. There are numerous challenges associated with MOEs, which I haven't fully explored in this article. For a deeper understanding of these challenges and potential solutions, I refer the readers to the insightful blogs mentioned in the introduction. They offer valuable insights into the intricacies of MOEs and the ongoing efforts to refine and optimize them.

As research progresses and MOEs evolve, their potential to revolutionize the field of AI becomes increasingly evident. In fact, GPT-4 is believed to be a MOE as well with 16 experts!